پرکاربردترین فرمول های انتگرال ریاضی

انتگرال گیری از مهم ترین مباحث ریاضیات در درس دیفرانسیل است که کاربردهای زیادی در علوم پایه، مهندسی و اقتصاد دارد. آشنایی با فرمول های انتگرال گیری به شما کمک می کند تا بتوانید برای محاسبه مساحت زیر محنی ها،اجسام سه بعدی، طول منحنی ها، میانگین مقادیر متغییر و… محاسباتی صحیح را انجام دهید.  در ادامه این مقاله ابتدا جدول کامل فرمول های انتگرال را مشاهده خواهید کرد و سپس با کاربردی ترین فرمول های انتگرال گیری معین، نامعین، توابع مثلثاتی، کسری و فرمول های انتگرال گیری ریاضی 1 آشنا خواهید شد. تا انتهای این مقاله همراه ما باشید.

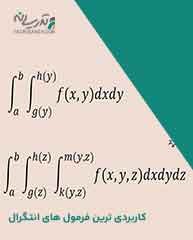
جدول کامل فرمول های انتگرال

وجود جدول کامل فرمول های انتگرال آن هم در یک مطلب با توجه به گستردگی فرمول های انتگرال گیری و اینکه فرمول های این مبحث در کتاب های گوناگونی بیان شده است، امکان پذیر نیست. با این حال در ادامه در قالب جدول های جداگانه به بیان مهم ترین فرمول های انتگرال گیری در مباحث مختلف پرداخته شده است.

فرمول های انتگرال کسری

آشتایی با فرمول های انتگرال کسری برای دانشجویان و دانش آموزانی که درس هایی از جمله دیفرانسیل، آمار و احتمالات، ریاضیات مهندسی، ریاضی عمومی 1 و 2 و... دارند، محاسباتی چالشی محسوب می شود. به همین علت باید حتما برای انجام محاسبات انتگرال های کسری از راهکارهایی از جمله تفکیک کسرها استفاده شود. با تفکیک کسرها، انتگرال گیری راحت تر می شود و در واقع کسرها به چند کسر ساده تر تبدیل می شوند که محاسبات انتگرال گیری آن را راحت تر می کند. در ادامه ابتدا در قالب جدولی فرمول های انتگرال گیری کسری بیان شده است و سپس مثال هایی برای تفکیک کسرها و انتگرال گیری آنها بیان شده است.

مثال فرمو های انتگرال کسری :

فرمول های انتگرال ریاضی 1

فرمول های انتگرال ریاضی 1 در دانشگاه و برای رشته های صنعتی و مهندسی کاربرد دارد. در ادامه در قالب جدولی به بیان مهم ترین و کاربردی ترین فرمول های انتگرال ریاضی یک پرداخته شده است.

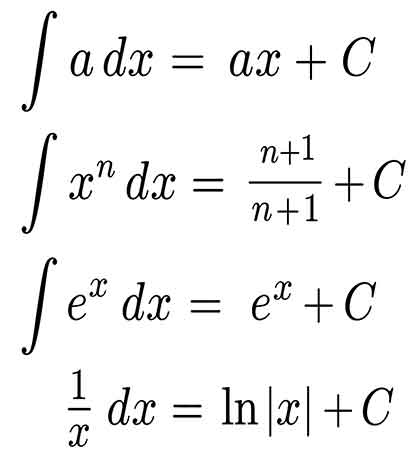
بیشتر بخوانید: معمای ریاضی تیزهوشان

فرمول های انتگرال معین

استفاده از فرمول های انتگرال معین زمانی است که برای انتگرال گیری محدوده مشخصی، تعیین شده باشد. به همین جهت تشخیص معین یا نامعین بودن انتگرال در استفاده از فرمول های انتگرال گیری نقشی بسیار مهم دارد. در ادامه به بیان کاربردی ترین فرمول های انتگرال گیری معین در قالب جدولی پرداخته شده است.

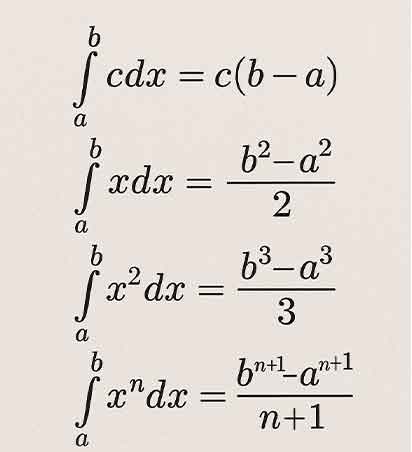
فرمول های انتگرال با مثال

خواندن فرمول های انتگرال با مثال به شما برای درک بهتر این درس کمک می کند. در ادامه برای انتگرال توابع مثلثاتی، توابع پایه، توابع کسری و... مثال های ساده و روانی بیان شده است. در ادامه همراه ما باشید.

فرمول های مشتق و انتگرال 

فرمول های مشتق و انتگرال بیشتر برای دروس دانشگاهی و محاسبات مهندسی مورد استفاده قرار میگیرد. در ادامه به بیان مهم ترین فرمول های مشتق و انتگرال خواهیم پرداخت تا شما به خوبی با فرمول های مهم مشتق و انتگرال گیری که به یکدیگر مرتبط هستند، آشنا شوید.

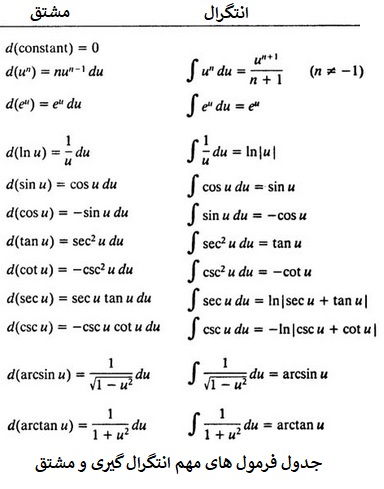
فرمول های انتگرال e

انتگرال e یکی از انتگرال های مهم و کاربردی در ریاضی است. در واقع e  عدد نپر محسوب می شود. البته اگر e در یک چند جمله ای یا یک تابع مثلثاتی ضرب شود، برای محاسبه انتگرال آن باید از روش جزء به جزء استفاده کرد. در ادامه همراه با مثالی به درک بهتر انتگرال e خواهید رسید.

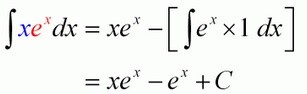
نکته: انتگرال e^x برابر e^x است.

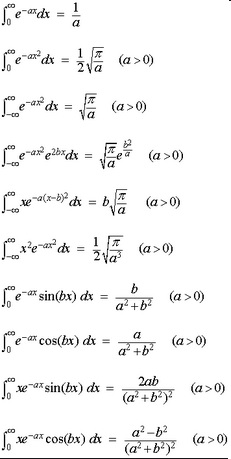
فرمول های انتگرال گیری پیش دانشگاهی

فرمول های انتگرال گیری پیش دانشگاهی یا همان سال دوازدهم بیشتر برای دانش آموزان رشته ریاضی کاربردی است و یادگیری و حفظ آن می تواند به موفقیت بیشتر دانش آموزان در آزمون های مهم منجر شود. در ادامه به بیان مهم ترین فرمول های انتگرال گیری سال دوازدهم پرداخته شده است. 

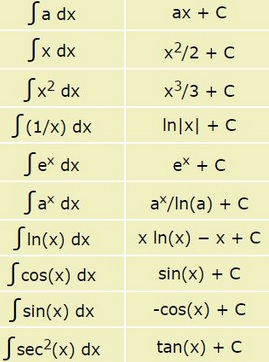
بیشتر بخوانید:بهترین روش مطالعه ریاضی کنکور

فرمول های انتگرال نامعین

فرمول های انتگرال نامعین برای انتگرال گیری زمانی مورد استفاده قرار میگیرد که برای انتگرال محدوده مشخصی تعربف نشده باشد. فرمول انتگرال تابع ثابت، کسری، نمائی، انتگرال ln، انتگرال سینوس، کسینوس و .... و همچنین برخی توابع رادیکالی در ادامه بیان شده است. باید به این نکته دقت داشته باشید که شما همه انتگرال ها را نمی توانید تنها با  استفاده از روابطی که در ادامه بیان شده است، به دست آورید و باید در کنار این فرمول ها از تکنیک های انتگرال گیری جزء به جزء یا تغییر و متغییر نیز استفاده کنید. 

مهم ترین فرمول های انتگرال مثلثاتی

آشنایی با مهم ترین فرمول های انتگرال مثلثاتی با توجه به کاربردی که این فرمول ها در مباحث حسابان و ریاضیات مهندسی وتوابع مثلثاتی دارند، برای دانش آموزان ریاضی و دانشجویان رشته های مهندسی امری ضروری محسوب می شود. در واقع بسیاری از مسائل فیزیک، مهندسی برق، مکانیک، نجوم و حتی پردازش سیگنال‌ها به انتگرال‌گیری از توابع مثلثاتی ختم می‌شود. به همین دلیل، دانستن فرمول‌های پایه‌ای انتگرال این توابع برای دانشجویان و علاقه‌مندان به ریاضیات ضروری است. در ادامه یک جدول کامل از مهم ترین فرمول های انتگرال توابع مثلثاتی قرار داده شده است تا شما برای حل و درک مسائل ریاضی خود بتوانید از این فرمول ها استفاده نمایید.

مهمترین فرمول های انتگرال مثلثاتی کدام اند؟

مهم ترین فرمول های انتگرال مثلثاتی عبارتند از:

1. انتگرال سینوس برابر با منفی کسینوس
2. انتگرال کسینوس برابر با سینوس
3. انتگرال تانژانت برابر با منفی لگاریتم طبیعی کسینوس
4. انتگرال کتانژانت برابر با لگاریتم طبیعی

این فرمول‌ها، اصلی‌ترین فرمول‌های انتگرال مثلثاتی محسوب می‌شوند.

بیشتر بخوانید:7 سوال سخت ریاضی

سخن آخر

در نهایت باید گفت که آشنایی با فرمول های کاربردی انتگرال گیری نه تنها در دوران دبیرستان و کنکور، حتی در دانشگاه و زمانی که شما در رشته های مهندسی مشغول به تحصیل باشید، کاربردی خواهد بود. در این مقاله با بیان فرمول های انتگرال معین، نامعین، کسری، توابع مثلثاتی و… شما را با کاربردی ترین فرمول های انتگرال گیری همراه با مثال های قابل فهم آشنا کردیم تا شما بدون نیاز ب کلیپ های آموزشی، نمرات خوبی را در امتحانات خود به دست بیاورید.